To submit your assignment, place a copy of your write-up (pdf preferred) and implementation into a directory called cs380hw2_lastname (substituting in your last name), then tar and gz this directory. Name the file cs380hw2_lastname.tar.gz. Submit it to me by attaching it to an e-mail with the subject of "CS380 Assignment 2 Lastname". Make sure you give me a hard-copy of your write-up for the assignment.
1.) [10 points] Exercise 6.5 from Newman
2.) [16 points total] Network Centrality
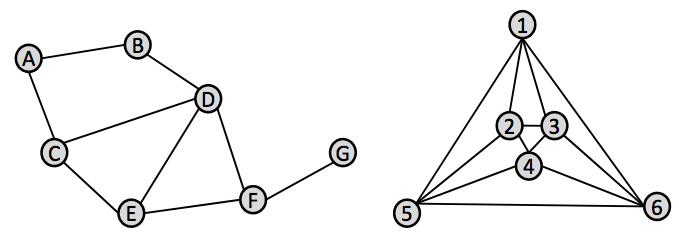
Answer each of these question based on the networks above. Show your work for partial credit and put a box around your answer.
a.) [4 pts] What is the diameter of the left network? The right network?
b.) [4 pts] What is the normalized degree centrality of vertices C and F in the left network?
c.) [4 pts] What is the normalized betweenness centrality of vertices C and F in the left network?
d.) [4 pts] Which network has larger centralization? (left or right)
3.) [14 points] Small World Networks
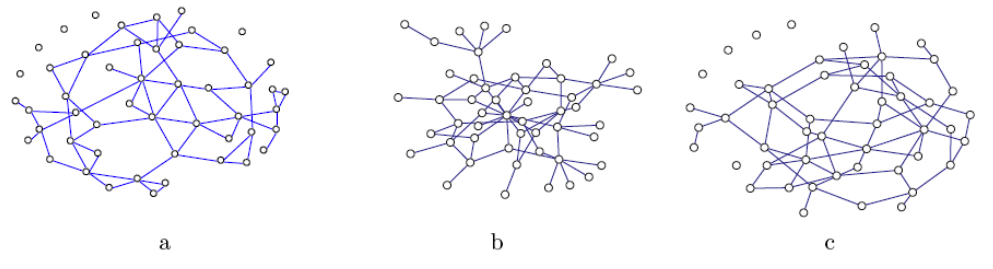
a.) [6 pts] Which of the following graphs has the highest clustering coefficient? (You don’t need to actually compute it!) Justify your answer.
b.) [8 pts] We introduced two variants of the Watts/Strogatz small world model (edge rewiring and edge addition). Which model leads to the larger clustering coefficient? The larger average path length? Justify your answers.
4.) [60 points] Network Centrality and Degree Distribution
In this problem you will be identifying important vertices in unknown networks using PageRank and Centrality.
I've provided the adjacency matrices for three graphs (dolphins.adj, imdb_prodco.adj, politicalblogs.adj). The format for the adjacency matrices is as follows:
#rows, #cols
source1, target1, edgeweight1
source2, target2, edgeweight2
source3, target3, edgeweight3
...The first line of the file specifies the dimensionality (rows and columns) of the matrix (i.e., number of vertices). Each subsequent line specifies the source vertex ID, the target vertex ID, and the edge weight. The vertices are identified by their number.
Analyze each of the graphs, providing the following information:
- A histogram plot of the in-degree of all vertices
- A histogram plot of the out-degree of all vertices
- A histogram plot of the PageRank of all vertices
- A histogram plot of the normalized degree centrality of all vertices
- The centralization of the graph
- A list of the 10 vertices with the highest in-degree and their values
- A list of the 10 vertices with the highest out-degree and their values
- A list of the 10 vertices with the highest PageRank and
their values
- A list of the 10 vertices with the highest degree
centrality and their values
You will need to implement methods for computing the
PageRank, normalized degree centrality, and
centralization. You may use a programming language of
your choice, but your implementation must read in the data
from the .adj files and output the following information (at a
minimum): the in-degree and out-degree of each vertex, the
PageRank of each vertex, the normalized degree centrality of
each vertex, and the centralization of the entire graph.
Given this output, you can use any program you like to compute
the histogram (Matlab, Gnuplot, your own program, etc.).
Your implementation can output the values for a histogram plot
as well.
How does the in-degree, out-degree, PageRank and normalized degree centrality of a vertex compare to each other?
Extra Credit [up to 15pts]
Compute the normalized betweenness centrality of the vertices
as well, and provide:
- a histograph plot of the normalized betweenness centrality
of all vertices, and
- a list of the 10 vertices with the highest betweenness centrality and their values.
You are welcome to use your implementation of Dijkstra's algorithm from assignment 1 to compute the geodesic path between various pairs of vertices. If you want a challenge, you could also implement the Floyd-Warshall algorithm to compute the shortest paths between all pairs of vertices in the network.
Exercises 2 and 3 were adapted from assignments by Qiaozhu
Mei, UMichigan.